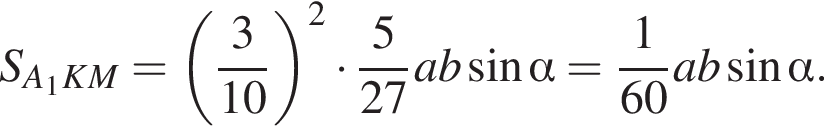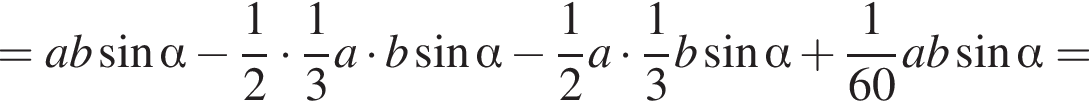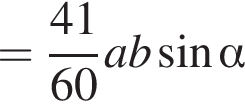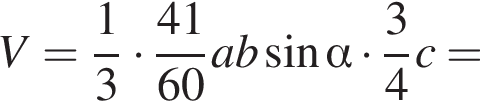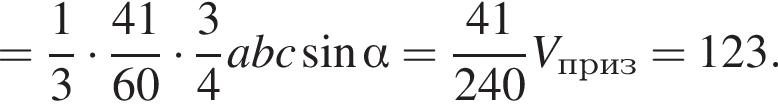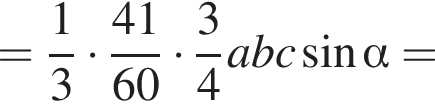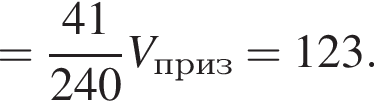Укажите номера прямоугольников, изображенных на рисунках 1−5, при вращении которых вокруг стороны AB получается цилиндр, осевым сечением которого является квадрат.
Централизованное тестирование по математике, 2017
Выразите 528 см 6 мм в метрах с точностью до сотых.
На рисунке изображен график движения автомобиля из пункта O в пункт K. Скорость движения автомобиля на участке NK (в км/ч) равна:
Выразите p из равенства 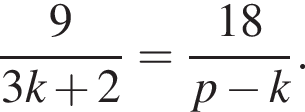

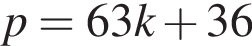
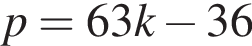

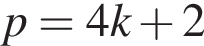
Значение выражения 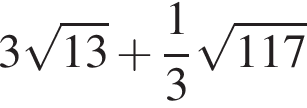 равно:
равно:
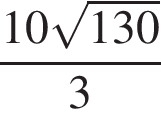
Последовательность (an) задана формулой n-ого члена 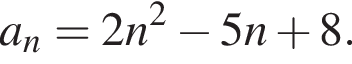 Второй член этой последовательности равен:
Второй член этой последовательности равен:
Значение выражения  равно:
равно:
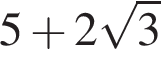
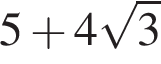
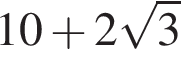
Среди данных утверждений укажите номер верного.
Дан треугольник ABC, в котором AC = 21. Используя данные рисунка, найдите длину стороны AB треугольника ABC.
Результат упрощения выражения 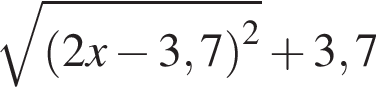 при −1 < x < 1 имеет вид:
при −1 < x < 1 имеет вид:
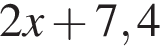
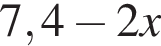
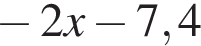
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Известно, что площадь этой фигуры составляет 36% площади некоторой трапеции. Найдите площадь трапеции в квадратных сантиметрах.
Определите остроугольный треугольник, зная длины его сторон (см. табл.)
| Треугольник | Длины сторон треугольника |
|---|---|
| ΔABC | 8 см; 15 см; 17 см |
| ΔMNK | 7 см; 12 см; 17 см |
| ΔBDC | 5 см; 8 см; 9 см |
| ΔFBC | 6 см; 8 см; 10 см |
| ΔCDE | 3 см; 6 см; 7 см |
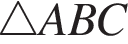




Купили c ручек по цене 1 руб. 2 коп. за штуку и 215 тетрадей по цене x коп. за штуку. Составьте выражение, которое определяет, сколько рублей стоит покупка.
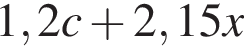
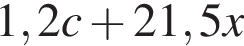



Среди предложенный уравнений укажите номер уравнения, графиком которого является парабола, изображенная на рисунке:
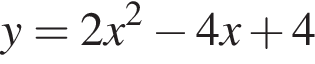
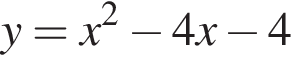
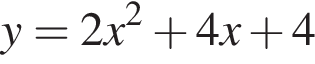
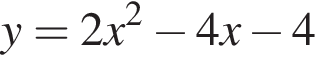
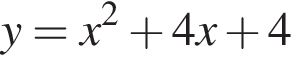
ABCDA1B1C1D1 — куб. Точки M и N — середины ребер AB и AD соответственно,
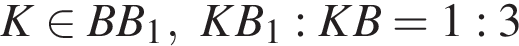 (см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
(см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства 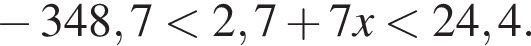
Через точку A высоты SO конуса проведена плоскость, параллельная основанию. Определите, во сколько раз площадь основания конуса больше площади полученного сечения, если SA : AO = 3 : 5.
Укажите (в градусах) наименьший положительный корень уравнения 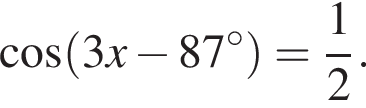
Для начала каждого из предложений A−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения |
|---|---|
| А) Окружность с центром в точке (−6; −4) и радиусом 9 задается уравнением: | 1) 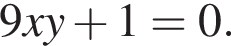 |
Б) Уравнением прямой, проходящей через точку (−6; 4) и параллельной прямой 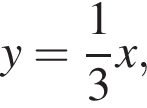 имеет вид: имеет вид: | 2) 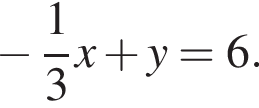 |
В) График обратной пропорциональности, проходящий через точку 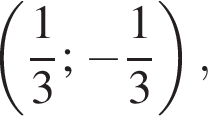 задается уравнением: задается уравнением: | 3) 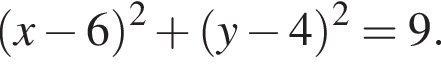 |
4) 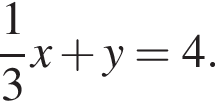 | |
5)  | |
6) 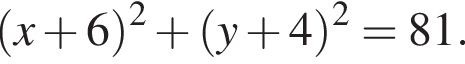 |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Конфеты в коробки упаковываются рядами, причем количество конфет в каждом ряду на 4 больше, чем количество рядов. Дизайн коробки изменили, при этом добавили 2 ряда, а в каждом ряду добавили по 1 конфете. В результате количество конфет в коробке увеличилось на 31. Сколько конфет упаковывалось в коробку первоначально?
Известно, что при a, равном −2 и 4, значение выражения 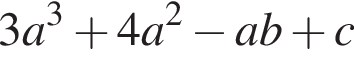 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Найдите произведение корней (корень, если он единственный) уравнения 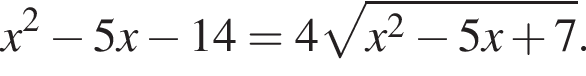
В параллелограмме с острым углом 45° точка пересения диагоналей удалена от прямых, содержащих неравные стороны, на расстояния ![]() и 5. Найдите площадь параллелограмма.
и 5. Найдите площадь параллелограмма.
Пусть x0 — наибольший корень уравнения 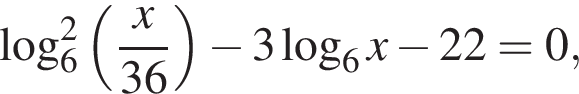 тогда значение выражения
тогда значение выражения ![]() равно ...
равно ...
Решите неравенство 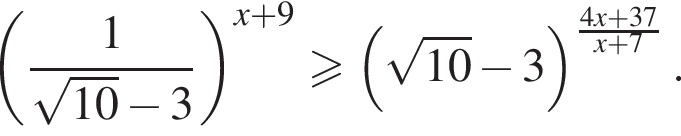 В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −5].
В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −5].
Найдите увеличенное в 9 раз произведение абсцисс точек пересечения прямой y = 4 и графика нечетной функции, которая определена на множестве  и при x > 0 задается формулой
и при x > 0 задается формулой 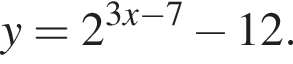
Найдите площадь полной поверхности прямой треугольной призмы, описанной около шара, если площадь основания призмы равна 4,5.
Найдите произведение наибольшего целого решения на количество целых решений неравенства 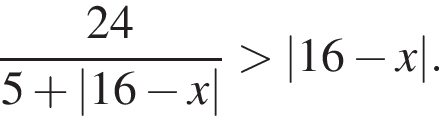
Первые члены арифметической и геометрической прогрессии одинаковы и равны 2, третьи члены также одинаковы, а вторые отличаются на 16. Найдите четвертый член арифметической прогрессии, если все члены обеих прогрессий положительны.
ABCDA1B1C1D1 — прямая четырехугольная призма, объем которой равен 720. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A1D1 и С1D1, так что A1M : MD1 = 1 : 2, D1N : NC1 = 1 : 2. Отрезки A1N и B1M пересекаются в точке K. Найдите объем пирамиды SB1KNC1, если 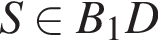 и B1S : SD = 3 : 1.
и B1S : SD = 3 : 1.

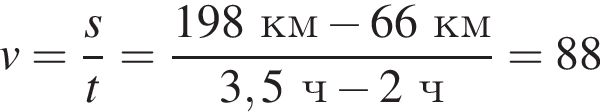 км/ч.
км/ч.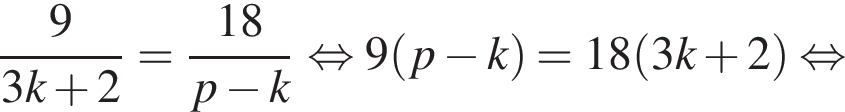
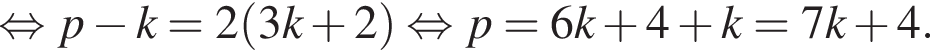
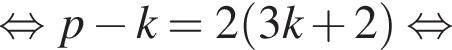
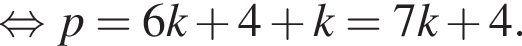
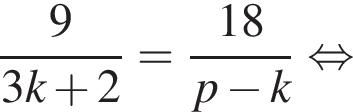
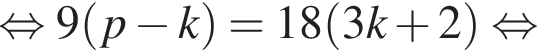
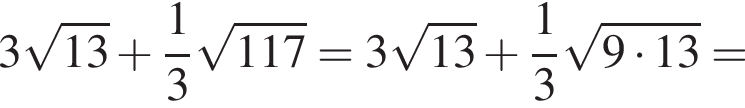
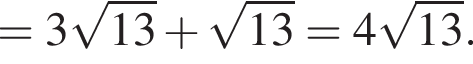
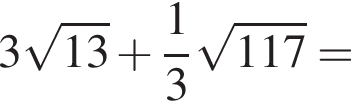
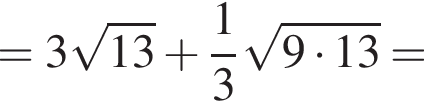
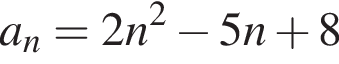 :
: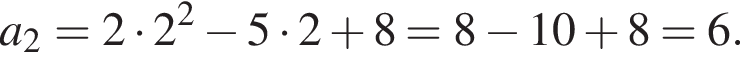
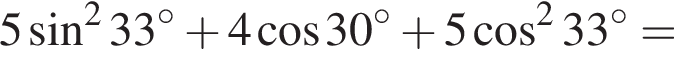
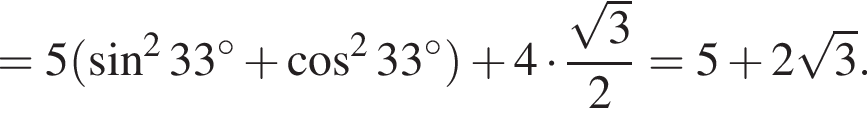
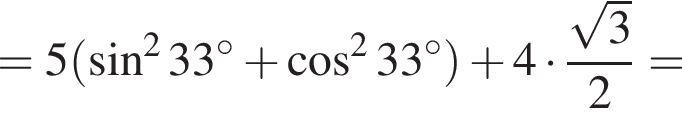
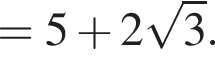
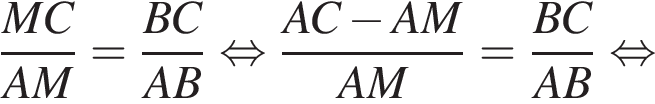
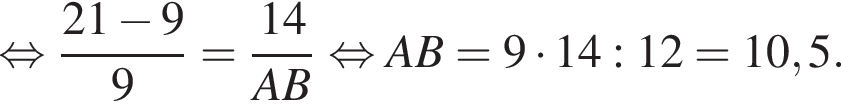
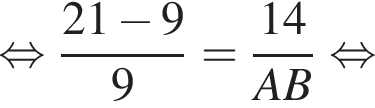
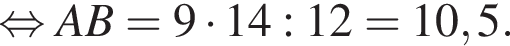
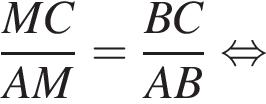
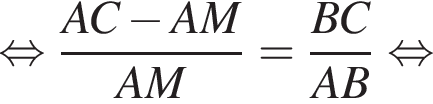
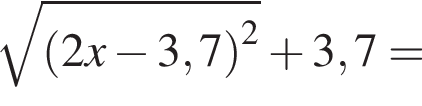
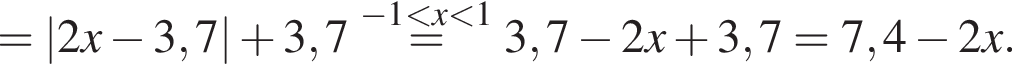
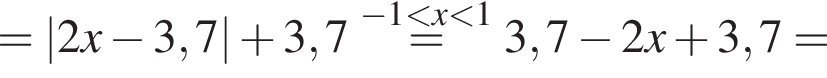
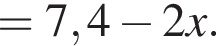
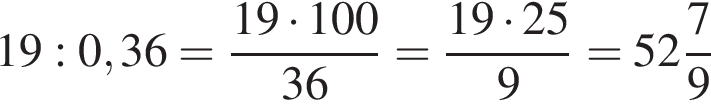 см2.
см2.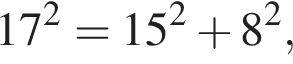 значит, треугольник прямоугольный.
значит, треугольник прямоугольный.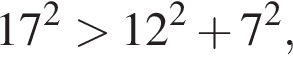 значит, треугольник тупоугольный.
значит, треугольник тупоугольный.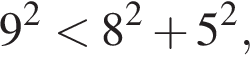 значит, треугольник остроугольный.
значит, треугольник остроугольный.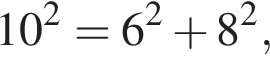 значит, треугольник прямоугольный.
значит, треугольник прямоугольный. значит, треугольник тупоугольный.
значит, треугольник тупоугольный.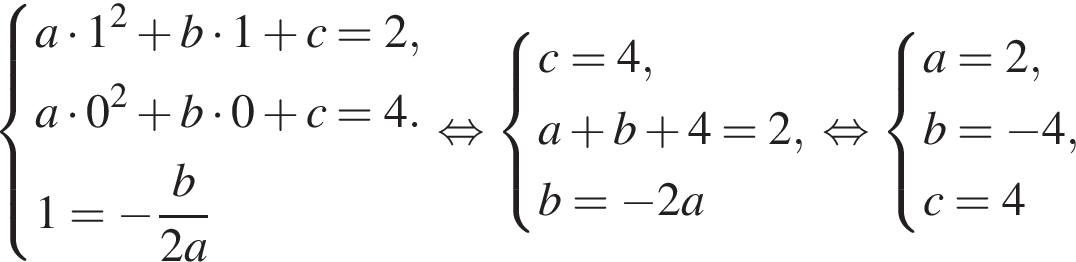
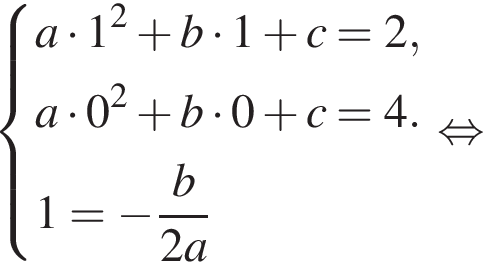
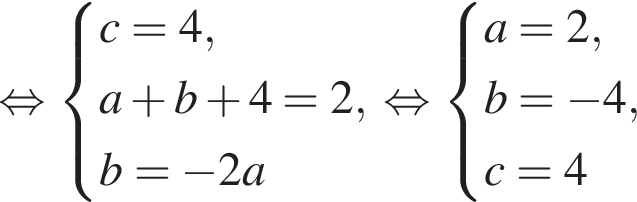
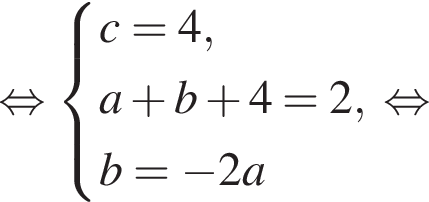
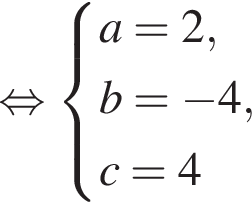
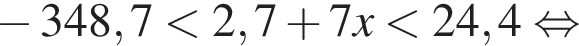
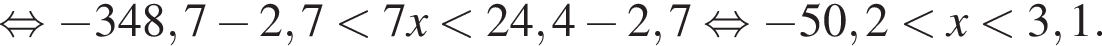
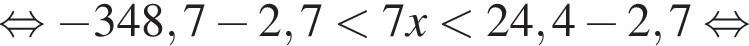
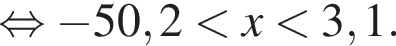
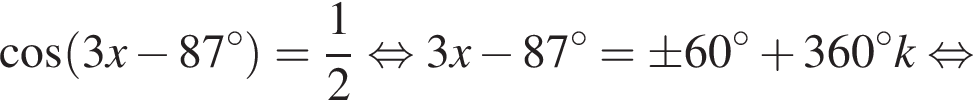
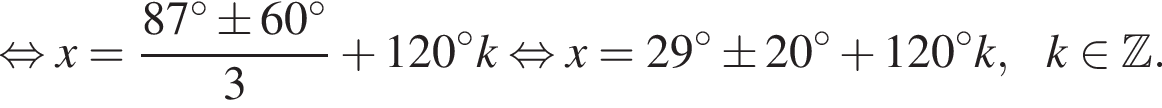
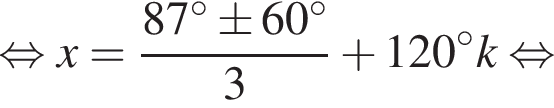
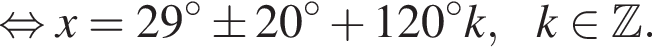
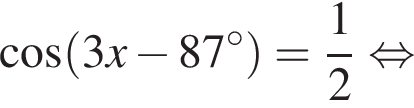
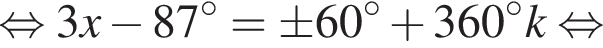
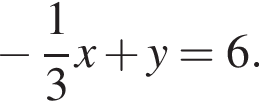
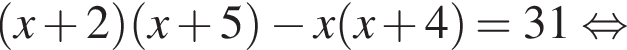
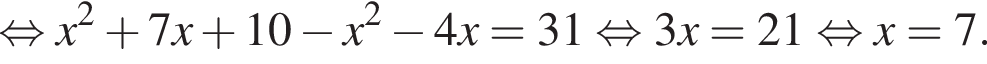

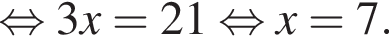
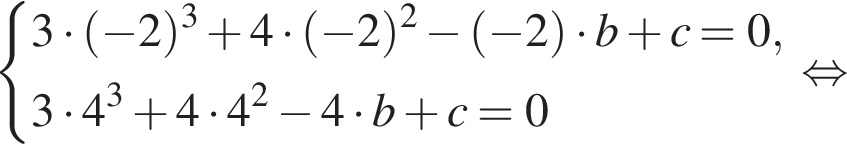
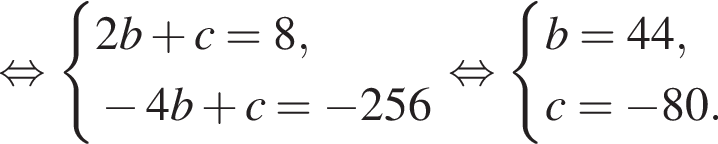
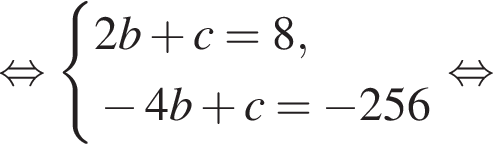
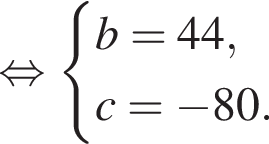

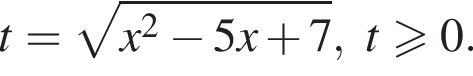 Имеем:
Имеем: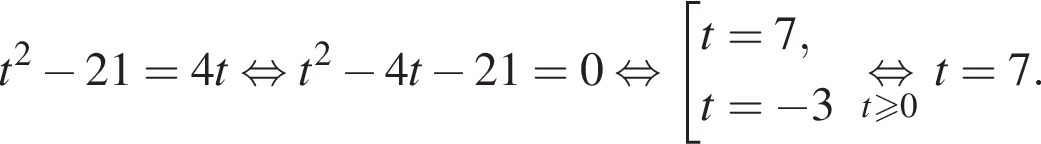
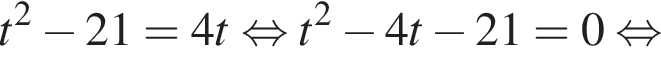
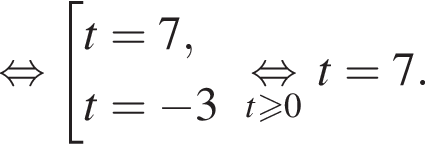
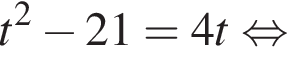
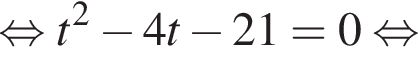
 Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −42.
Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −42.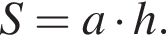 Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 5 = 10:
Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 5 = 10: 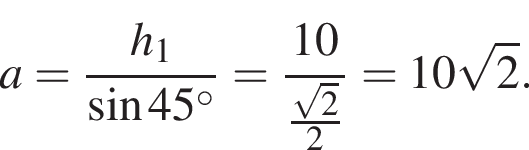 Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту
Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту 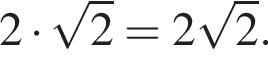
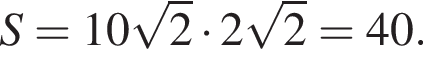
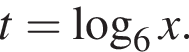
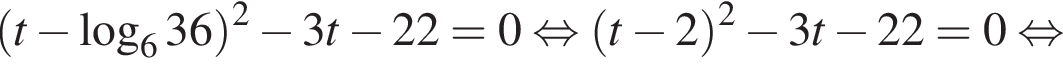
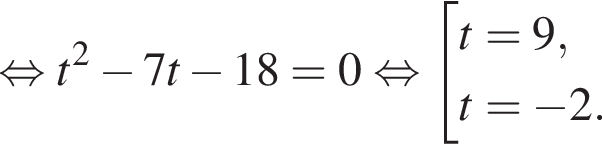
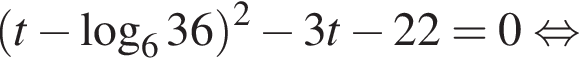
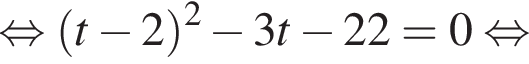
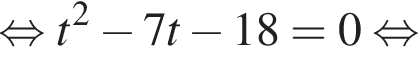
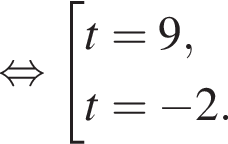
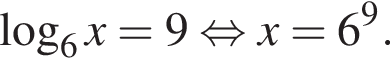 Тогда
Тогда 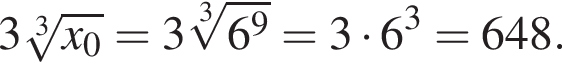
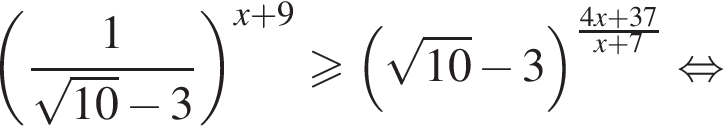
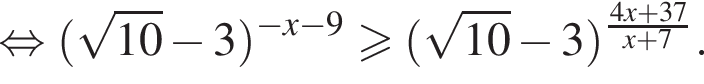
 неравенство будет выполняться при
неравенство будет выполняться при 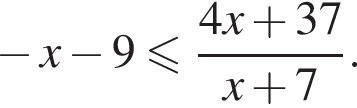 Имеем:
Имеем: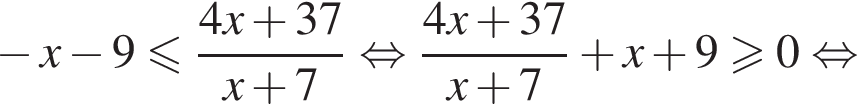
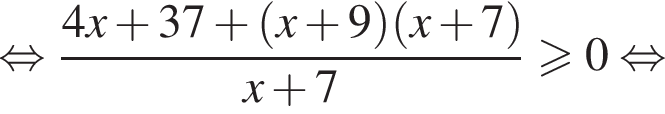
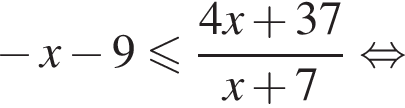
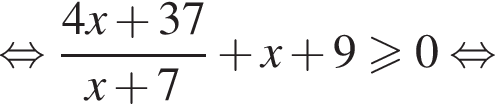
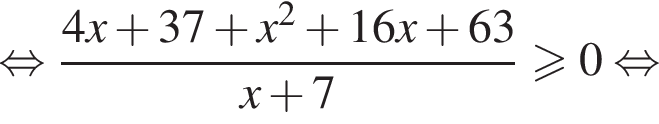
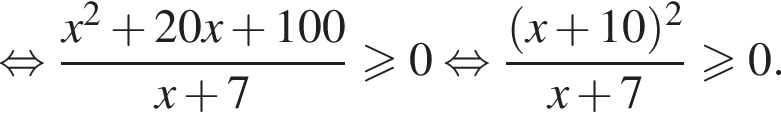
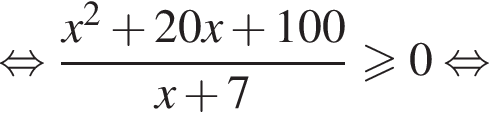
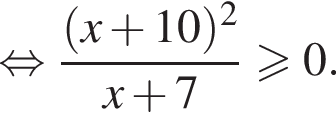

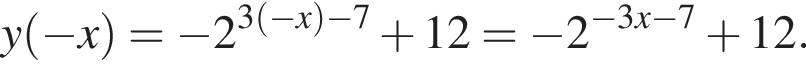
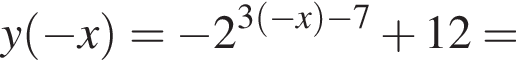
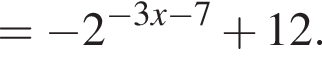
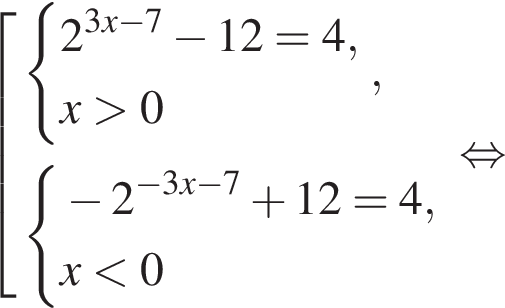
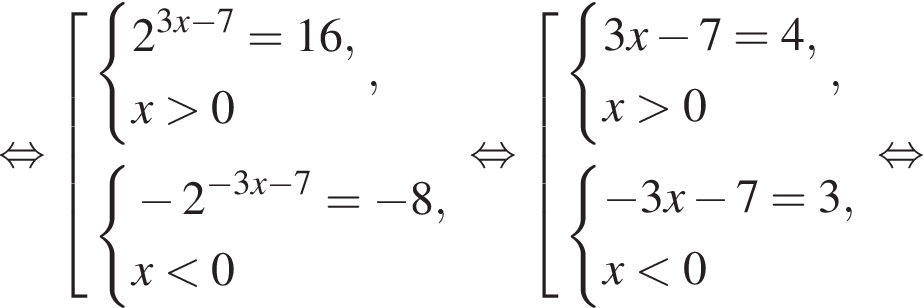
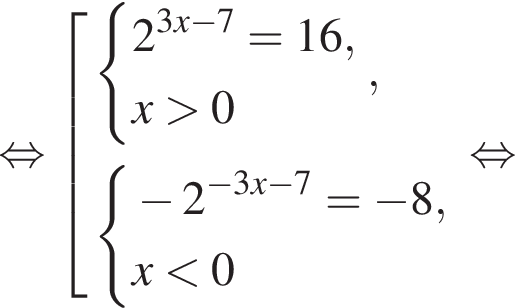
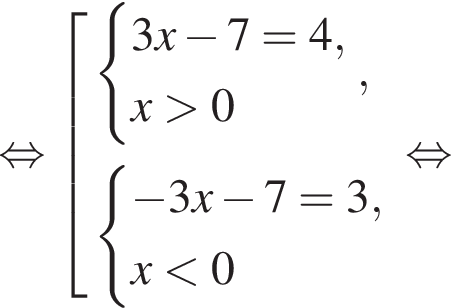
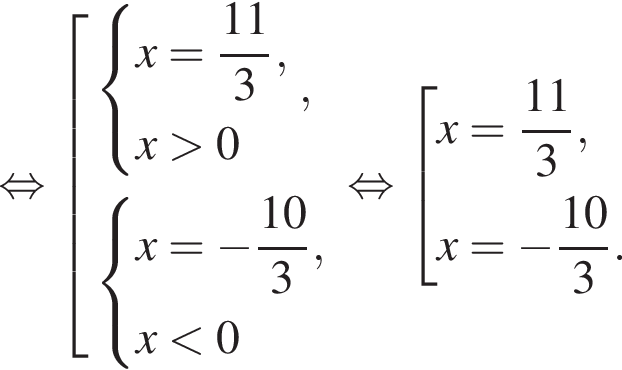
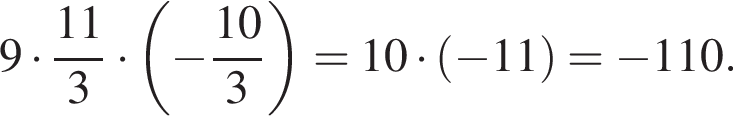
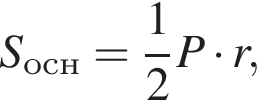 где P — периметр основания призмы, r — радиус шара. Кроме того, высота призмы равна диаметру шара, т. е.
где P — периметр основания призмы, r — радиус шара. Кроме того, высота призмы равна диаметру шара, т. е. 
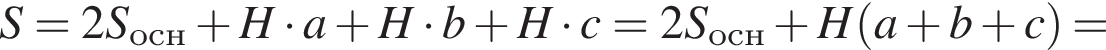
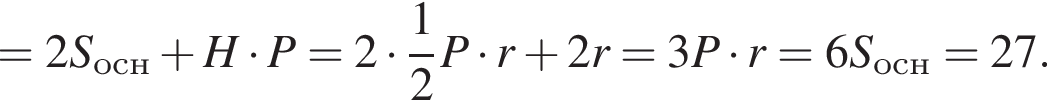
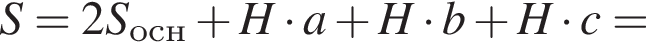
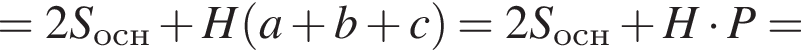
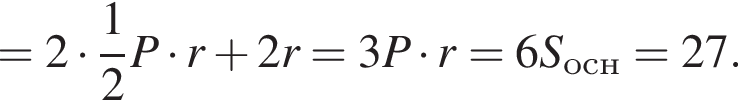

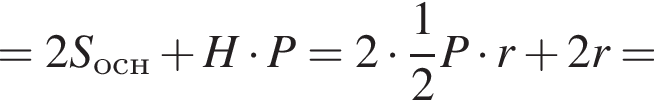
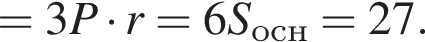


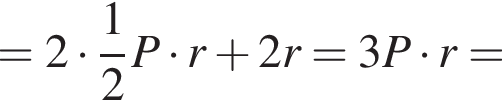

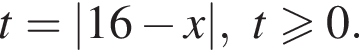 Имеем:
Имеем: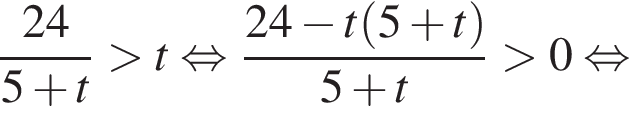
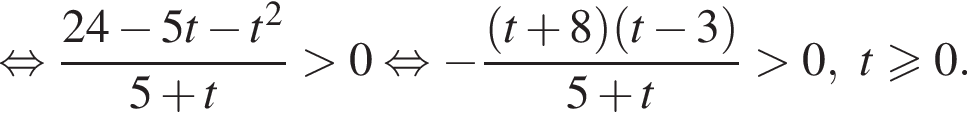
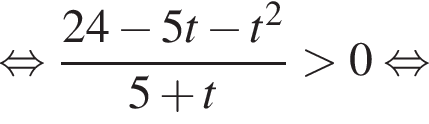
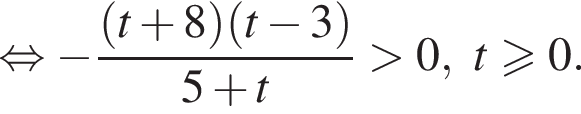
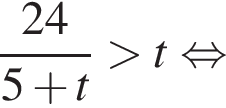
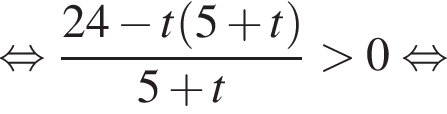
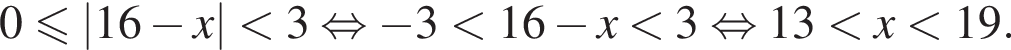
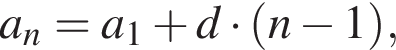 геометрическая прогрессия задается уравнением
геометрическая прогрессия задается уравнением 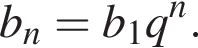
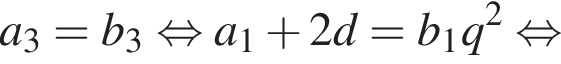
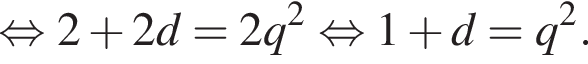
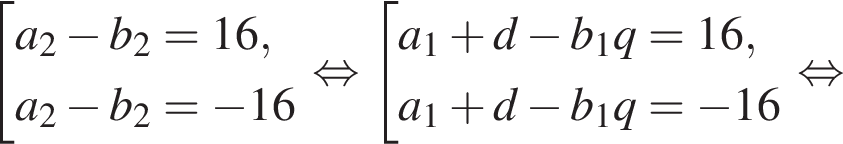
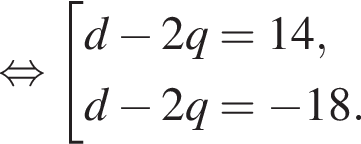
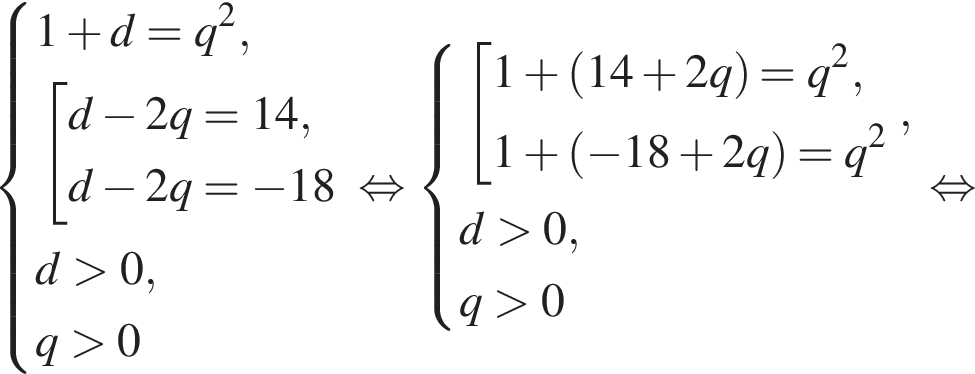
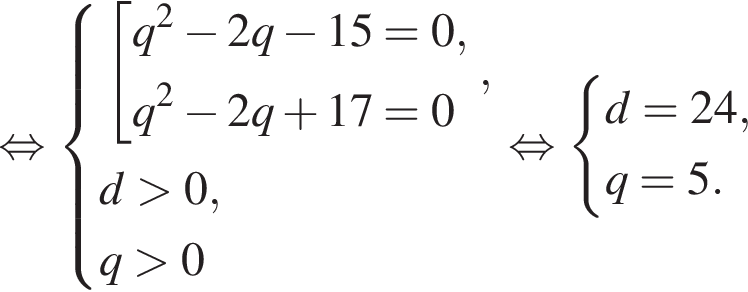
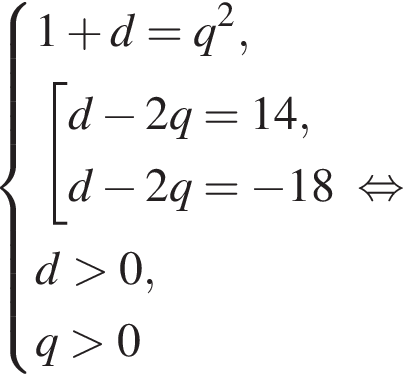
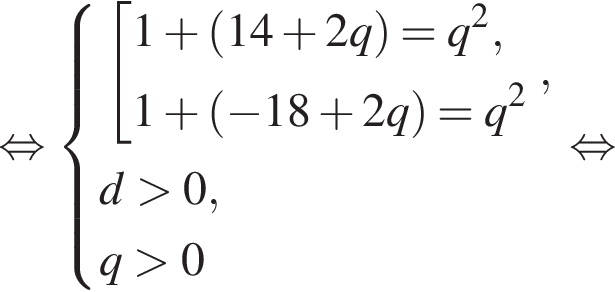
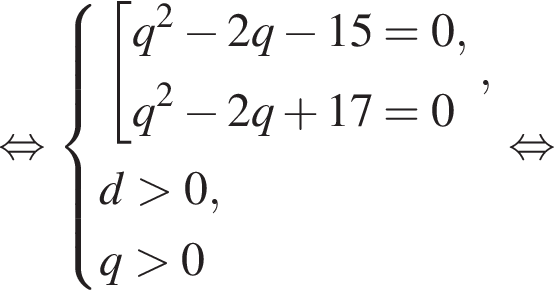
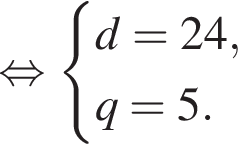
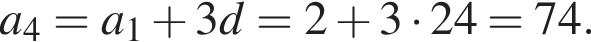
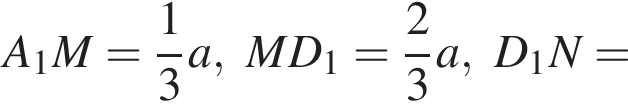
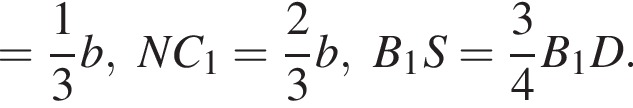
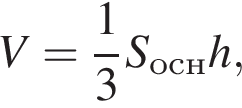 где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на рисунке.
где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на рисунке.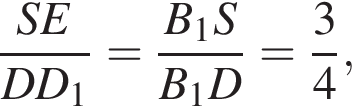 поэтому
поэтому 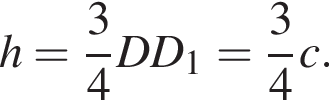

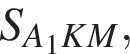 для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1. Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому:
для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1. Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому: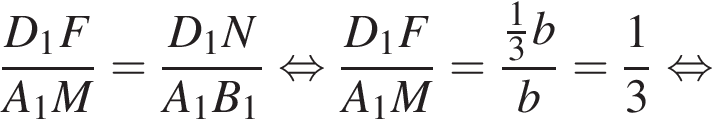
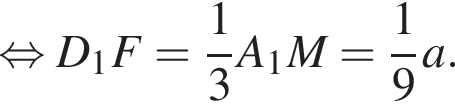

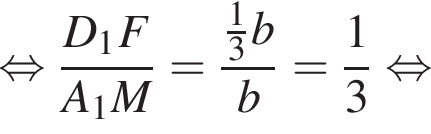
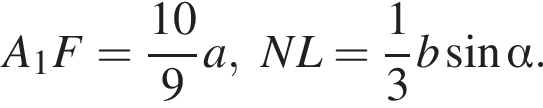 Соответственно, площадь треугольника A1NF равна
Соответственно, площадь треугольника A1NF равна 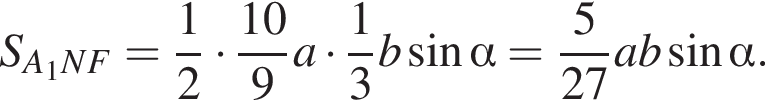 Треугольники A1KM и A1NF подобны с коэффициентом подобия:
Треугольники A1KM и A1NF подобны с коэффициентом подобия: 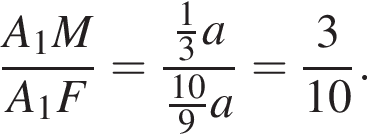 Отсюда площадь треугольника A1KM равна
Отсюда площадь треугольника A1KM равна